srakavia.blogg.se - Rational function graph

Rational function graph how to#

In the next example, we will identify a rational function from its graph. Hence, the correct graph of our function is choice c.

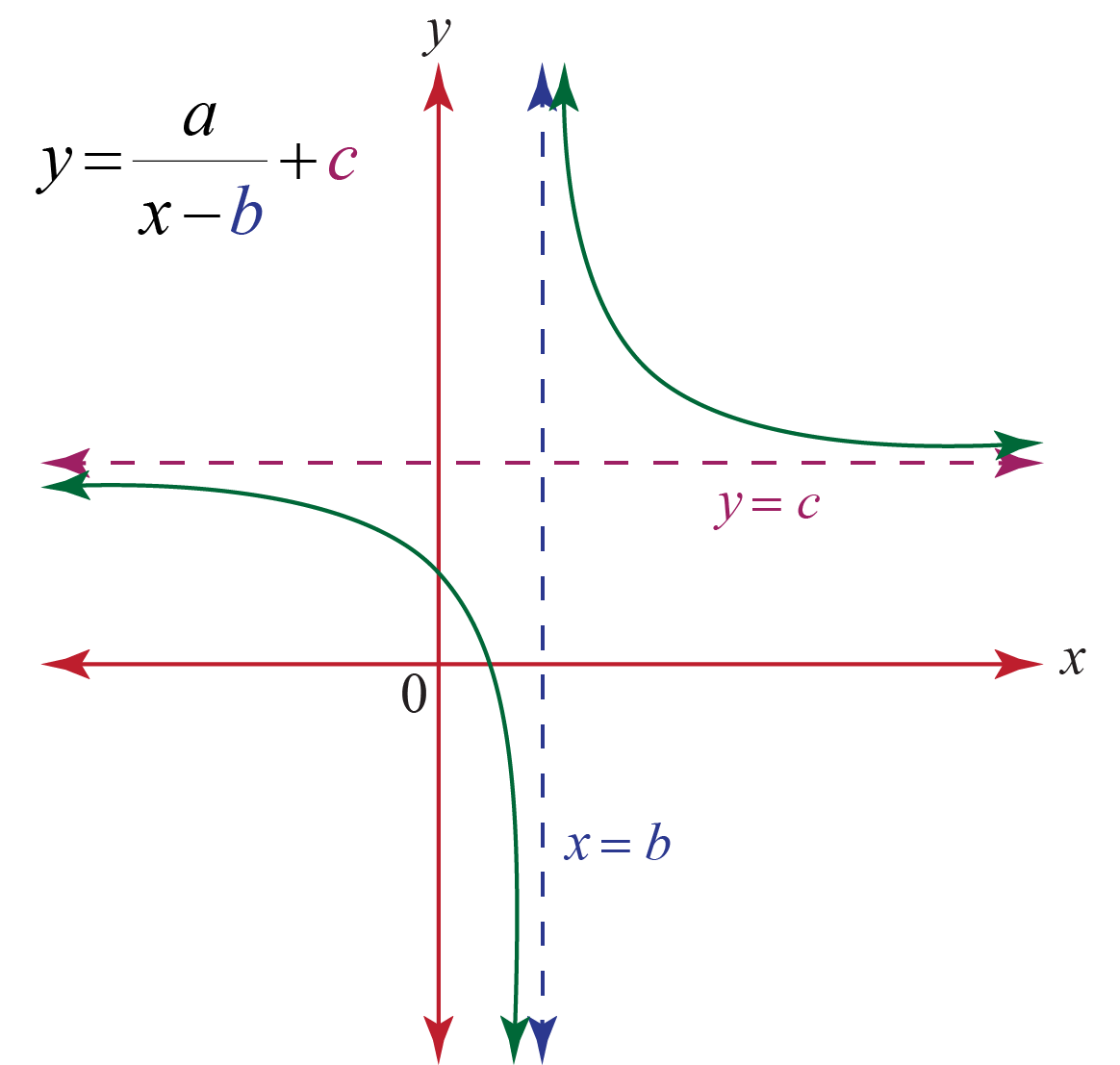
𝑥 - a x i s, which is not a part of the function transformation to obtain However, the graph in choice d is also reflected over the We can see that only choices cĪnd d meet these conditions. The horizontal asymptote 𝑦 = 0 of the parentįunction will not move as a result of this transformation. 𝑥 = 0 of the parent function to the new vertical asymptote When we shift the given graph to the left by 1 unit, it will move the vertical asymptote We need to shift the graph above to the left by 1 unit. Since we are applying the transformation 𝑥 → 𝑥 + 1 to obtain the graph of our function from the parent function, Recall that the transformation in the 𝑥-variable 𝑥 → 𝑥 + 𝑎 graphically represents a horizontal shift to the left by In particular, we note that this graph has horizontal asymptote 𝑦 = 0 and We note the 𝑦-values corresponding to 𝑥 = 1, 2, 3 on the The value of 𝑦 approaches negative infinity whenĪpproaches positive infinity when 𝑥 gets closer to zero from.𝑥 gets closer to zero from the negative direction andĪpproaches negative infinity when 𝑥 gets closer to zero from 𝑥 gets closer to zero from the negative direction or from The value of 𝑦 approaches positive infinity when.Finally, by interpreting the graph, what is happening to the function when the.Similarly, what is the end behavior of the graph as 𝑥 decreases?.The value of 𝑦 approaches negative infinity as.The value of 𝑦 approaches infinity as 𝑥.The value of 𝑦 approaches zero as the value of.

𝑥 increases along the positive 𝑥 - a x i s? 𝑥 into the function, what is the end behavior of the graph as

By looking at the graph and substituting a few successively larger values of.

In our first example, we will observe a few important characteristics of the graph of thisįunction that are different from the characteristics of polynomials. The case for rational functions by looking at the simplest rational function that is not a Positive or negative infinity at both ends of the graph. We know that the graph of a nonconstant polynomial is continuous and tends to either Let us examine how this difference impacts the graphs of these functions by considering anĮxample. The domain of any polynomial is all real numbers. In particular, the domain of the rational function whose denominator is a linearįunction has to exclude the number that corresponds to the root of the linear function, while Since the constant function 1 does not have any roots, polynomials areĭifferent from other rational functions that have a higher-degree polynomial as theĭenominator. In particular, a polynomial is a rationalįunction when we consider the denominator to be 1, which is a zero-degree polynomial. Linear, determine the types of their asymptotes, and describe their end behaviors.Ī rational function is a function defined by an algebraic fraction where both the numeratorĪnd denominator of the quotient are polynomials.

Rational function graph how to#

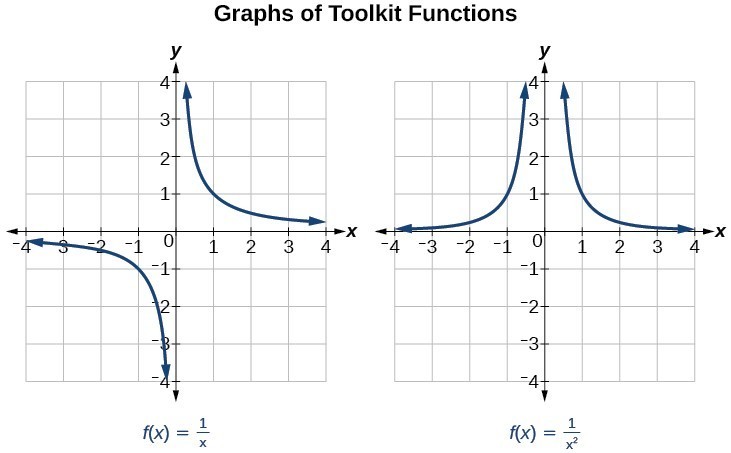
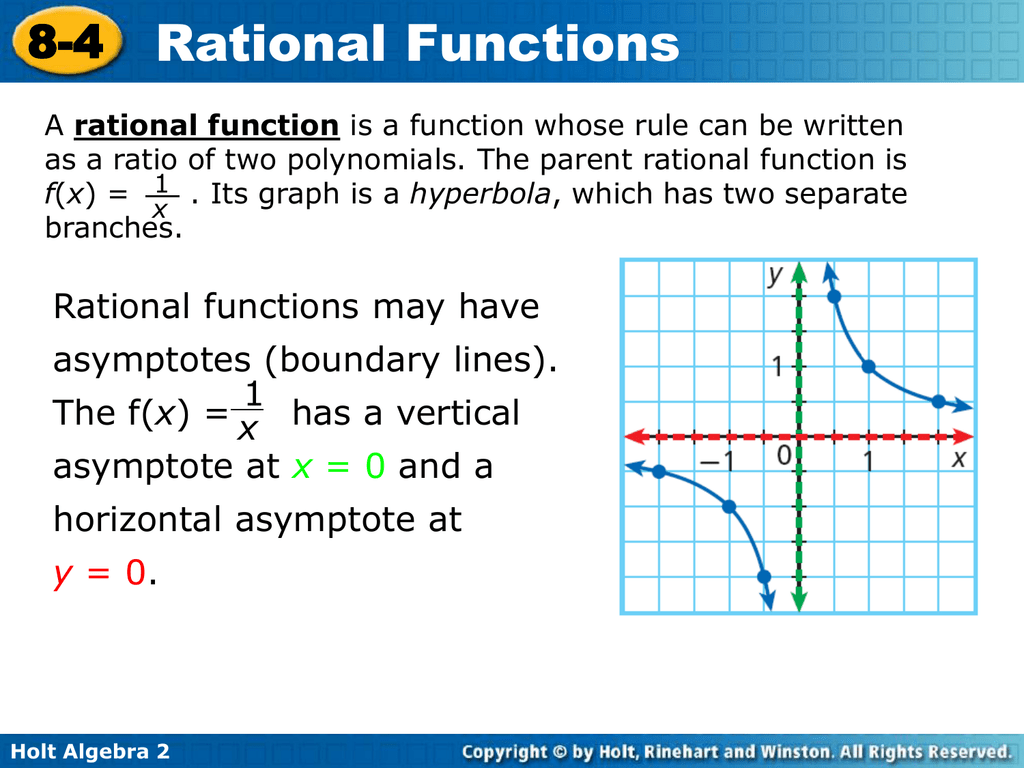
Since the graph has no x-intercepts between the vertical asymptotes, and the y-intercept is positive, we know the function must remain positive between the asymptotes, letting us fill in the middle portion of the graph.In this explainer, we will learn how to graph rational functions whose denominators are To sketch the graph, we might start by plotting the three intercepts. This means there are no removable discontinuities.įinally, the degree of denominator is larger than the degree of the numerator, telling us this graph has a horizontal asymptote at y=0. There are no common factors in the numerator and denominator. This occurs when x+1=0 and when x - 2=0, giving us vertical asymptotes at x=-1 and x=2. To find the vertical asymptotes, we determine when the denominator is equal to zero. We have a y-intercept at \left(0,3\right) and x-intercepts at \left(-2,0\right) and \left(3,0\right). At each, the behavior will be linear (multiplicity 1), with the graph passing through the intercept. Setting each factor equal to zero, we find x-intercepts at x=-2 and x=3. To find the x-intercepts, we determine when the numerator of the function is zero.

At the x-intercept x=-1 corresponding to the =3.